Back to http://completecenter.gmu.edu/index.html
TASK: Students were asked to arrange 12 tiles into straight rows for an audience to watch a play Click for the instructional ppt Rolling Valley GMU Lesson_study_Ppt
SOL 3.6 Students will represent multiplication and division using area models and sets, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor five or less.
Goals:
- Commutative Property – to recognize a x b = b x a and a + b = b + a (foundation for commutative property)
- Introduce to rectangular arrays
- These concepts will be the foundation for learning about area, multiplication, multiple arrays (factors)
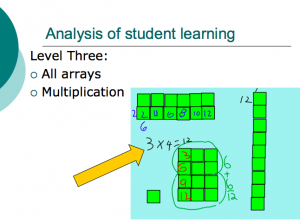
Previous Knowledge
- Skip counting
- Commutative property of addition
- Vocabulary – row, column, rectangle, array
SOL 3.6 Students will represent multiplication and division using area models and sets, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor five or less.
Anticipate:
Methods:
Count by ones, Count by twos
Count by fours, Count by threes
Students may not come up with 2 orientations of each array
Students will come up with 1 x 12 and then split apart.
Some students may know all the factors already and make the arrays and multiplication statements.
Misconceptions: Not making even rows, not keeping a rectangle, not understanding that a square is a rectangle.
Errors: Making uneven rows, and using incorrect numbers of tiles to make arrays. Not able to draw the representation on recording sheet, not coming up with all arrays that are possible for the number, labeling arrays incorrectly. Students making array with tiles, but not copying the array on the paper.
Resources: 12 inch tiles for each pair of students, inch graph paper for each pair, and pencils and erasers.
Students will work in pairs. The students will be paired by varying ability levels; most students will be paired heterogeneously making sure that low IEP/ESOL students will have support with similar ability levels.
Recording/reporting: Showing array using tiles, drawing arrays on graph paper, students will label the dimensions on drawings.
Use smartboard to share student ideas with entire class.
Extension – 16 tiles for early finishers to try various arrays; 4 additional tiles for a total of 20 tiles during self-selecting time.
| Monitor: Introduce situation with movie theatre or classroom placement of chairs; begin with a group of four chairs on Smartboard so there are limited choices.Focus questions: Asking students: Are there any other rectangles you can build? Did you use all your tiles? Is that a rectangle? How did you count your tiles? You can turn it. That’s not a rectangle. Can we turn it? Do you have all the different rectangles and how do you know?We see and hear: All arrays with rows and columns clearly labeled. Arrays should be numbered in order of completion.Are students counting by ones or twos? Are students skip counting or counting by groups? Is it partner work or one dominant child? Do students recognize that rectangles can be rotated to create another array?Questions to assess: Have you made all the different rectangles? What other ways could this be made? What do you notice about these two rotations? Are the two rotations the same rectangle? How are they the same, and how are they different?Questions to advance student understanding:What numbers can you start with that will give you more rectangles, and what numbers can give you fewer rectangles? Do all bigger numbers have more rectangles? What numbers can you build that will only have two arrays /rectangles? What patterns are you seeing? What patterns do you see in the numbers that you have drawn? Can anyone restate what so-and so just said?Questions to encourage students: Did anyone find a different rectangle? How did you count your tiles? Do you have all the possible arrays? How do you know?
Engagement: If student is unsure encourage him to model what the teacher did on the board independently. Then build slowly adding two tiles at a time. Early Finishers: Give the students four more tiles and encourage them to create and record as many arrays as possible using the 16 tiles. What patterns can you discuss with the class? Non-Mathematical Aspects: Students will be given one minute of exploration time with the tiles before the task begins. Encourage students to find all the arrays instead of focusing on one array. Students should only use pencils instead of markers or crayons. Extension: Students will be given additional tiles (for a total of 20) and will self-select a number to create and label arrays for that number. Before beginning, students should predict how many arrays they think they will be able to create. Students will share their results with the class orally. |
| Selecting/ Sequencing:Solution Paths:First sharing group – counting by ones, skip counting. This group will share first because these solutions are based on prior knowledge.Second sharing group – breaking the tiles into groups or using some other organizing system. This group will demonstrate different ways of thinking.Third sharing group – discussing factors and multiplication facts. These students already can recognize the connection between arrays and multiplication. |
| Connections: The solution paths will help the students bridge the gap between addition and multiplication by showing the relationship between the two. We will hear students say, “Oh order doesn’t matter.” By having students number the arrays in order of completion, it will allow us to see if they create one array and then automatically recognize the corresponding array (commutative property). We will hear students explain what they did, i.e. “I used three rows of four,” or “ I turned this to make four rows of three,” or “two rows of six is the same of six rows of two,” and “six rows of two and three rows of four show the same number.” Arrays are drawn and correctly labeled. We hope to see all possible combinations drawn and labeled. We can close by asking students how they knew if they found all the possible arrays. |