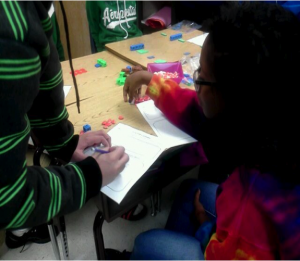Where do equations come from, where do they go and how do they get there?
The lesson goal and objectives:
Given a word problem and manipulatives, students will be able to write and solve a two-step equation. By doing this we hope they will also gain a better understanding of where equations come from and why we use them. We also hope this will help them to understand the process of solving an equation and why we do the steps that we do.
SOL 8.15a The student will solve multi-step linear equations in one variable on one side and two-sides of the equation.
The essential math concepts:
Learning Goals and Big Ideas
Too often students are focused on the answer without giving thought to the process that gets them to the final step, placing a priority on the abstract rather than the understanding of the concrete.
Hands on math is common in early education – grades Kindergarten through third grade and begins to transition to pencil and paper soon after. This push to the abstract is often at the cost of a true understanding of number sense.
Common Misconceptions
If a concept was covered in previous grade levels, students have mastered the concepts and are ready to build on those fundamentals of mathematics.
If a student can read a problem, write and solve an equation, they have an essential understanding of the mathematics.
Middle school students do not need manipulatives.
Vertical Connections
The student will be able to:
5.18
a. investigate and describe the concept of variable
b. write an open sentence to represent a given
mathematical relationship using a variable
c. model one-step linear equations in one variable
using addition and subtraction
6.19 Investigate and recognize
a. the identity properties for addition and multiplication
b. multiplicative property of zero
c. inverse property of multiplication
7.14
a. solve one- and two- step linear equations in one variable
THE RESEARCH LESSON
Students are grouped in pods of four. Manipulatives are set in the middle of the pods. Manipulatives are foam Algebra Tiles, two colored chips, dried beans painted red on one side and white on the other, snap cubes in various colors and colored chips.
The Warm Up
Students are given 3 expressions and asked to model each with the toys (manipulatives) in their pod.
“Using the manipulatives at your table, model the following expressions”
2 + 4 6 – 5 3×6
EXPLORE
Once the students have had time to model the expressions in the warm-up, they explain their models and their ideas are recorded on the SmartBoard.
Time is given for the students to verbalize what they were thinking when they constructed the models.
Exploration Experience
The instructor provides the students with a problem and manipulatives. The students are asked to use the manipulatives to create a model that shows the problem and the solution. Students are allowed to work with their group to get ideas, but each student is responsible for creating and documenting their own model.
Doing the MATH
Some students had no trouble representing the algorithm with the manipulatives. Other students struggled with using the objects to represent units and/or variables.
After students had enough time to create a model, they were asked to move around the room to look and hear how their peers had represented the same problem. The students were asked to illustrate two models that their peers has used that were different from their own. Following the “Gallery Walk” a teacher lead discussion provided the students a chance to compare, contrast and verbalize their thought process.
After the class discussion, students were presented with a second problem. They were again asked to model the problem but were required to use a different form of manipulative in an attempt to create a different model.
Once students had modeled the second problem, the instructor introduced the connection between modeling the problem and the writing and solving of an equation.
Students were given small cards, each representing a part of the equation, and asked to match the cards to the manipulatives they had used to represent the problem.
To provide closure to the day’s class, students were asked to write their answer s to the following questions:
How do you know that the equation you created is the equation that represents the problem you were given?
Solve the equation you wrote using the steps that you normally use to solve an equation.
How do these steps relate to the model you created? Did you get the same answer that you got using your model?
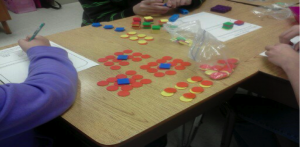
Students with different models created. As you notice, students improvised with signs and may not see the connection between the integer and operation in the photo below.
Students beginning to model the first problem and notice the combination of manipulative used. One struggle for the students was relating the meaning of each manipulative throughout the solving.
Students recognizing the equation as a model and being able to define their variable perhaps as a different manipulative.
Use of Manipulatives
The concrete manipulatives provided were two colored beans, two sided counters, snap cubes, different color chips and algebra tiles. Virtual manipulates could also have been used. Pictures or diagrams could have been a number line.
ELABORATE
Connections between representations and strategies.
The students had to communicate about their models through both verbal explanation and a drawing of their model. Many were quick to create a model but had a difficult time explaining their work. Most students who could not explain their model had a model that didn’t quite accurately represent the information.
In their explanation, many students wanted to talk in terms of a variable right away, but others didn’t even consider a variable and simply made sense of the different values as they corresponded to each other. Some students even tried to physically write out an equation with their modeling pieces instead of representing numbers and variables. This is likely because they were uncomfortable with a new way of looking at the problems.
Connections between representations and strategies continued…
Some of the students were able to explain that they would subtract a value from both sides of the model and then divide by the number of hops. Other students showed that they still were not sure of the process of subtracting from both sides and then dividing. They wanted to divide and then subtract.
Real World Relevance
Hopefully students will begin to realize that they can always make a model or a least draw a diagram to help solve problems whether in math or other subjects.
The idea here is that students use their new knowledge to build their growing knowledge base.
EVALUATE
A the end of the class period, the students were given a third problem to solve individually. For this problem they had to create a model, write an equation and solve the problem. In doing this they were able to demonstrate whether or not they had gained a true understanding of how to use modeling as a tool and whether or not they understand the relationship between concrete modeling and equation solving.
After completing the third problem, they had to answers three questions:
Observe that students need a concrete reminder of the operations. The abstract connection of the term and operations has to be supported for many students by the signs.
Learning Goal
The student will be able to take a word problem, form a model/diagram, write an equation and solve the equation feeling confident about their model and use of mathematics.
They will also have a better understanding of how equations represent real situations. Many students are able to solve an equation on paper but do not understand how that relates to anything relevant in the real world.
Learning Product
The learning product is the student’s work on the third word problem.
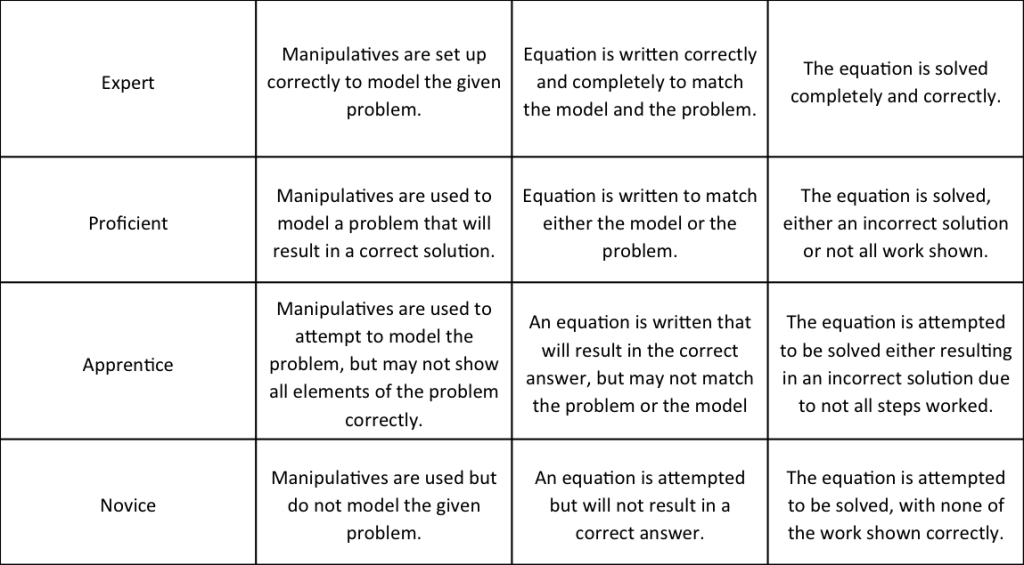
The rubric below was used to help determine how students did.